Advanced Consolidation¶

In this section we explain consolidation in depth. Specifically, we describe the consolidation algorithm and all the configuration parameters that can be used to tune the consolidation performance to the user application.

Fragment clean up¶

Before the consolidation algorithm begins, TileDB applies a simple optimization in a pre-processing step, which may lead to great performance benefits depending on the “shape” of the existing fragments. Specifically, TileDB identifies dense fragments whose non-empty domain completely covers older adjacent (dense or sparse) fragments, and directly deletes the old fragment directories without performing any actual consolidation.

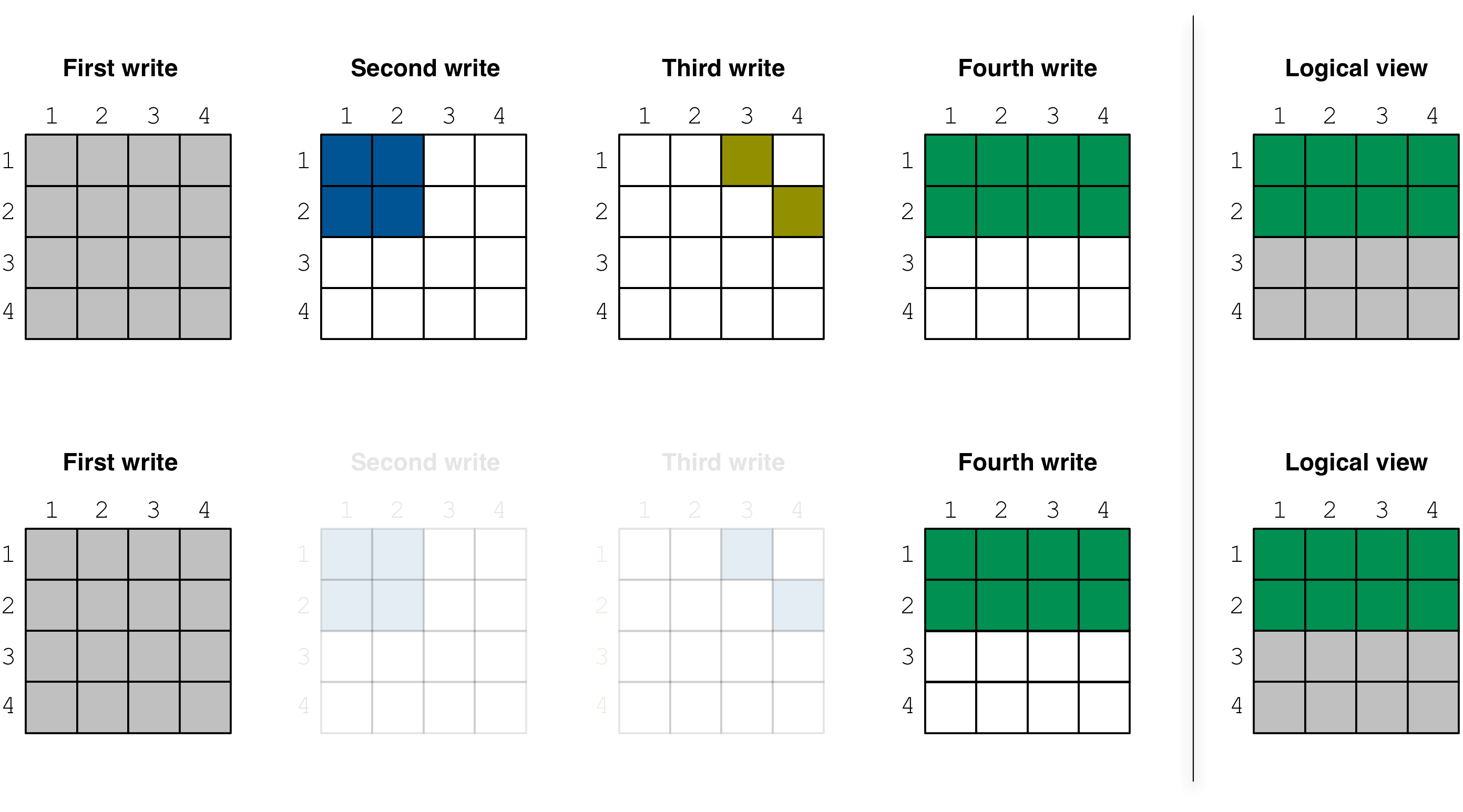
This clean-up process is illustrated with an example in the figure below. Suppose the first fragment is dense and covers the entire array, i.e., [1,4], [1,4], the second is dense and covers [1,2], [1,2], the third is sparse as shown in the figure, and the fourth one is dense covering [1,2], [1,4]. Observe that, if those four fragments were to be consolidated, the cells of the second and third fragment would be completely overwritten from the cells of the fourth fragment. Therefore, the existence of those two fragments would make no difference to the consolidation result. Deleting them altogether before the consolidation algorithm commences will result in boosting the algorithm performance (since fewer cells will be read and checked for overwrites).

Consolidation algorithm¶

The consolidation algorithm is performed in steps. In each step, a subset of adjacent (in the timeline) fragments is selected for consolidation. The algorithm proceeds until a determined number of steps were executed, or until the algorithm specifies that no further fragments are to be consolidated. The choice of the next fragment subset for consolidation is based on certain rules and user-defined parameters, explained below. The number of steps is also configurable, controlled by sm.consolidation.steps.

To configure the consolidation algorithm, you must create and set a config object with the desired parameters, and pass it as argument in the consolidation function as follows:

C++

Context ctx;
Config config;
config["sm.consolidation.steps"] = 3;
Array::consolidate(ctx, array_name, config);

Python

config = tiledb.Config()
config["sm.consolidation.steps"] = 3;
tiledb.consolidate(array_name, config)

Now let us focus on a single step, during which the algorithm must select and consolidate a subset of fragments based on certain criteria:

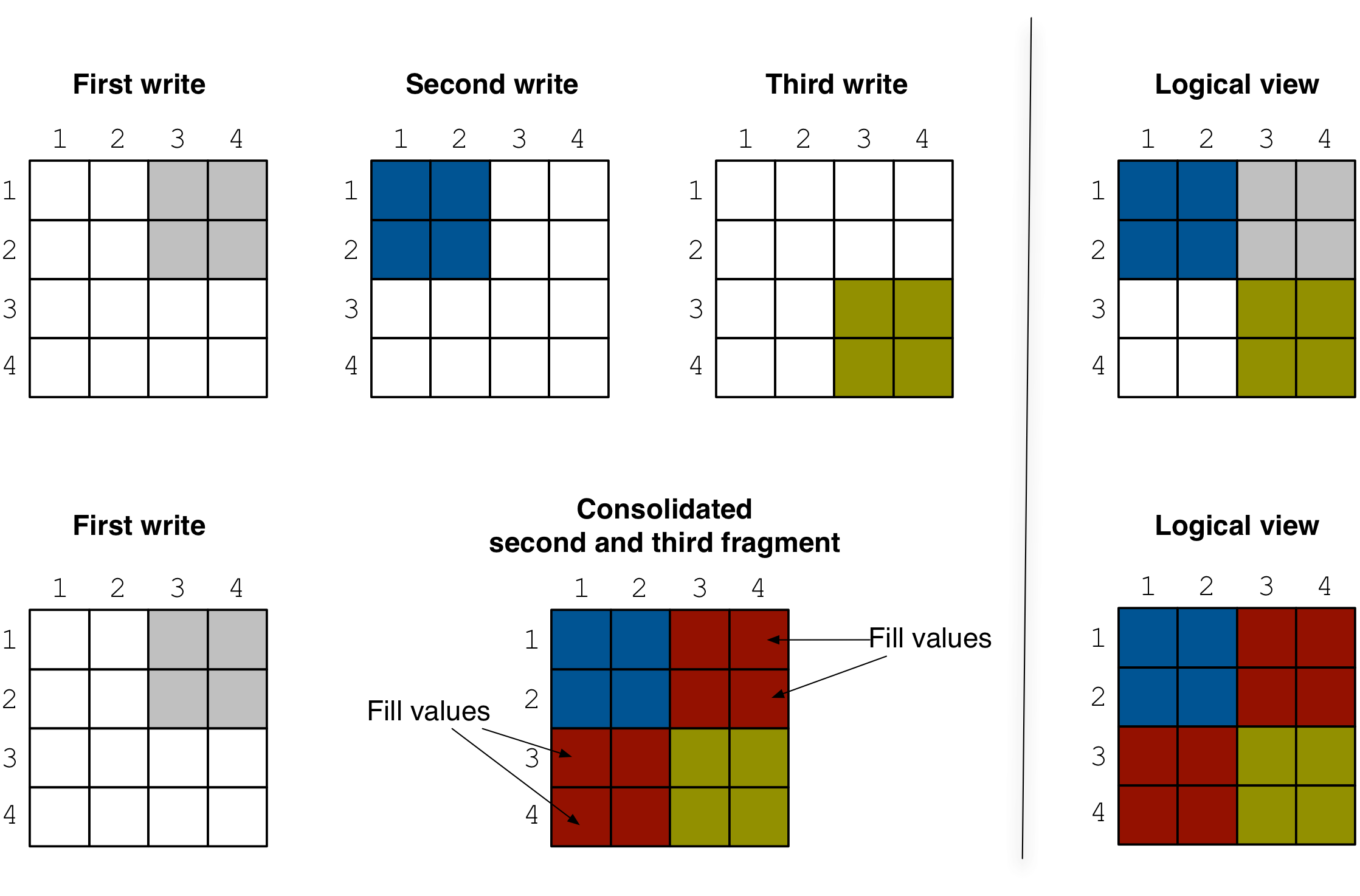
The first criterion is if a subset of fragments is “consolidatable”, i.e., eligible for consolidation in a way that does not violate correctness. Any subset consisting of solely sparse fragments is always consolidatable. However, if a fragment subset contains one or more dense fragments, TileDB performs an important check; if the union of the non-empty domains of the fragments (which is equal to the non-empty domain of the resulting consolidated fragment) overlaps with any fragment created prior to this subset, then the subset is marked as non-consolidatable. Recall that the fragment that results from consolidating a subset of fragments containing at least one dense fragment is always a dense fragment. Therefore, empty regions in the non-emtpy domain of the consolidated fragment will be filled with special values. Those values may erroneously overwrite older valid cell values. Such a scenario is illustrated in the figure below. The second and third fragments are not consolidatable, since their non-empty domain contains empty regions that overlap with the first (older) fragment. Consequently, consolidating the second and third fragment results in a logical view that is not identical to the one before consolidation, violating correctness. This criterion detects and prevents such cases.

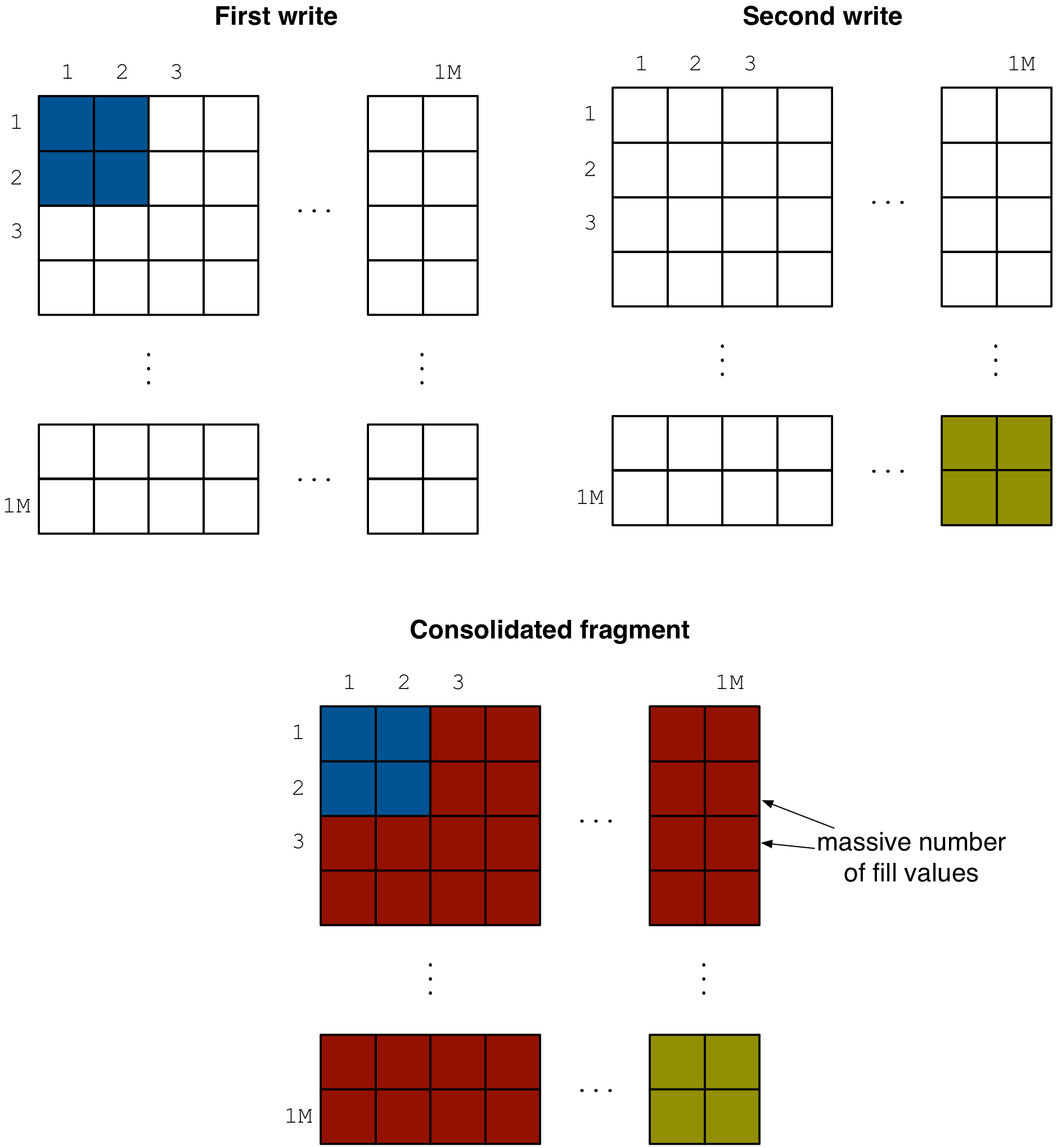
The second criterion is the comparative fragment size. Ideally, we must consolidate fragments of approximately equal size. Otherwise, we may end up in a situation where, for example, a 100GB fragment gets consolidated with a 1MB one, which would unnecessarily waste consolidation time. This is controlled by parameter sm.consolidation.step_size_ratio; if the size ratio of two adjacent fragments is larger than this parameter, then no fragment subset that contains those two fragments will be considered for consolidation.
The third criterion is the fragment amplification factor, applicable to the case where the fragment subset to be consolidated contains at least one dense fragment. If the non-empty domain of the resulting fragment has too many empty cells, its size may become considerably larger than the sum of sizes of the original fragments to be consolidated. This is because the consolidated fragment is dense and inserts special fill values for all empty cells in its non-empty domain (see figure below). The amplification factor is the ratio between the consolidated fragment size and the sum of sizes of the original fragments. This is controlled by sm.consolidation.amplification, which should not be exceed for a fragment subset to be eligible for consolidation. The default value 1.0 means that the fragments will be consolidated if there is no amplification at all, i.e., if the size of the resulting consolidated fragment is smaller than or equal to the sum of sizes of the original fragments. As an example, this happens when the non-empty domain of the consolidated fragment does not contain any empty cells.

The fourth criterion is the collective fragment size. Among all eligible fragment subsets for consolidation, we must first select to consolidate the ones that have the smallest sum of fragment sizes. This will quickly reduce the number of fragments (hence boosting read performance), without resorting to costly consolidation of larger fragments.
The final criterion is the number of fragments to consolidate in each step. This is controlled by sm.consolidation.step_min_frags and sm.consolidation.step_max_frags; the algorithm will select the subset of fragments (complying with all the above criteria) that has the maximum cardinality smaller than or equal to sm.consolidation.step_max_frags and larger than or equal to sm.consolidation.step_min_frags. If no fragment subset is eligible with cardinality at least sm.consolidation.step_min_frags, then the consolidation algorithm terminates.

The algorithm is based on dynamic programming and runs in time O(max_frags * total_frags), where total_frags is the total number of fragments considered in a given step, and max_frags is equal to the sm.consolidation.step_max_frags config parameter.

Note

When computing the union of the non-empty domains of the fragments to be consolidated, in case there is at least one dense fragment, the union is always expanded to coincide with the space tile extents. This affects criterion 1 (since the expanded domain union may now overlap with some older fragments) and 2 (since the expanded union may amplify resulting consolidated fragment size).

Performance tips¶

The best scenario for maximizing the performance of reads is to have a single fragment. The only way to result in a single fragment is by (i) performing a single write (which may not be possible in applications where the data is much larger than RAM), (ii) writing in global order, i.e., appending data to your fragments (which may not be possible in applications where the data do not arrive in global order), and (iii) frequently consolidating your fragments, which is the most reasonable choice for most applications. However, properly tuning consolidation for an application may be challenging. Therefore, below we provide a few tips for maximizing the consolidation performance.

Perform dense writes in subarrays that align with the space tiles. In this case, the consolidation algorithm writes to the consolidated fragment in global order, instead of row-/col-major order, which is generally faster.
Update the (dense) array by trying to rewrite the same dense subarrays. This helps the pre-processing clean up process, which will try to delete older fully overwritten fragments rapidly without performing consolidation.
For sparse arrays (or sparse writes in dense arrays), perform writes of approximately equal sizes. This will lead to balanced consolidation.
It may be a good idea to invoke consolidation after every write, tuning sm.consolidation.step_min_frags, sm.consolidation.step_max_frags and sm.consolidation.steps to emulate the way LSM-Trees work. Specifically, choose a reasonable value for sm.consolidation.step_min_frags and sm.consolidation.step_max_frags, e.g., 2-20. This will ensure that only small number of fragments gets consolidated per step. Then you can set the number of steps (sm.consolidation.steps) to something large, so that consolidation proceeds recursively until there is a single fragment (or very few fragments). If consolidation is invoked after each write, the consolidation cost will be amortized over all ingestion processes in the lifetime of your system. Note that in that case, the consolidation times will be quite variable. Sometimes no consolidation will be needed at all, sometimes a few fast consolidation steps may be performed (involving a few small fragments), and sometimes (although much less frequently), consolidation may take much longer as it may be consolidating very large fragments. Nevertheless, this approach leads to a great amortized overall ingestion time resulting in very few fragments and, hence, fast reads.
Increase the buffer size used internally during consolidation. This is controlled by config parameter sm.consolidation.buffer_size, which determines the buffer size used per attribute when reading from the old fragments and before writing to the new consolidated fragment. A larger buffer size increases the overall performance.