Negative and Real Domains

Unlike most software managing arrays, in TileDB you can define negative or even real coordinate spaces, which means that TileDB allows you to store values in cells identified by negative or real coordinates.

Negative domains

Negative domains can be used in both dense and sparse arrays. They behave identically to what we have seen so far. Here is a simple example defining 2D domain [-2, 1], [-1, 2] with a 2x2 space tiling.

C++

Context ctx;
Domain domain(ctx);
domain.add_dimension(Dimension::create<int>(ctx, "rows", {{-2, 1}}, 2))
      .add_dimension(Dimension::create<int>(ctx, "cols", {{-1, 2}}, 2));

Python

dom = tiledb.Domain(tiledb.Dim(name="rows", domain=(-2, 1), tile=2, dtype=np.int32),
                    tiledb.Dim(name="cols", domain=(-1, 2), tile=2, dtype=np.int32))

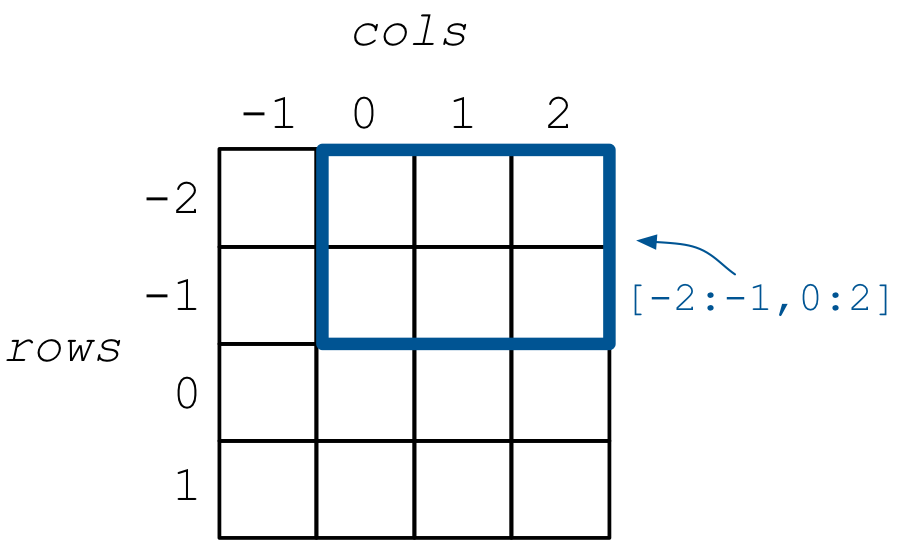
This creates the 2D array shown in the figure below.

As expected, tiling starts from the beginning of the domain, i.e., the tiles in the example are [-2, -1], [-1, 0], [-2, -1], [1, 2], [0, 1], [-1, 0], and [0, 1], [1, 2]. Moreover, slicing is used as you have already learnt, allowing you to use ranges over negative coordinates as well, e.g., [-2, -1], [0, 2] as shown in the figure.

Real domains

Real domains (of type float32 or float64) can be used only in sparse arrays, as dense arrays are defined only on integer domains. Recall that we defined an array cell as being uniquely identified by a coordinate tuple equal to the dimensionality of the array. This definition encompasses real coordinate spaces as well.

One of the motivating applications for real domains is storing geospatial locations as longitude/lattitude pairs, which are float32 values. The global lon/lat coordinate space is [-180.0, 180.0], [-90.0, 90.0]. Then each geolocation is a pair (lon, lat).

We can create such a domain very easily as follows:

C++

Context ctx;
Domain domain(ctx);
domain.add_dimension(Dimension::create<float>(ctx, "lon", {{-180.0, 180.0}}, 0.1))
      .add_dimension(Dimension::create<float>(ctx, "lat", {{-90.0, 90.0}}, 0.1));

Python

dom = tiledb.Domain(tiledb.Dim(name="lon", domain=(-180.0, 180.0), tile=0.1, dtype=np.float32),
                    tiledb.Dim(name="lat", domain=(-90.0, 90.0), tile=0.1, dtype=np.float32))

The figure below shows how such an array looks like. Observe that each non-empty cell is now better perceived as a point in the domain. Also notice that in the figure lon is the first dimension, which appears as the X-axis, and lat is the second, which appears as the Y-axis (this is easier to think about rather than in terms of rows/cols as in the integer domain case).

Space tiling (set to 0.1 x 0.1 in our example) is used in the same way as for integer domains in sparse arrays, i.e., solely for determining the global (physical) order of the points. Finally, you can issue slices with real-valued ranges, e.g., [11.34, 45.11], [-23.0001, 1.456] shown in the figure.